As sine definition takes center stage, this opening passage beckons readers into a world crafted with mathematical precision, ensuring a reading experience that is both absorbing and distinctly original.

Prepare to delve into the mathematical intricacies of the sine function, unraveling its properties, applications, and profound significance across diverse fields.

Sine Function Overview

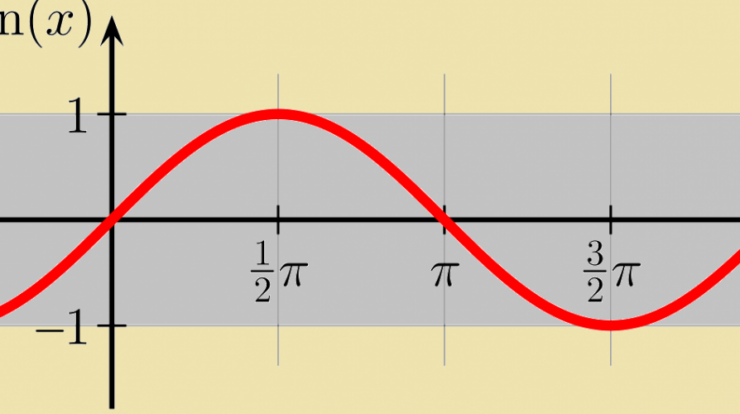
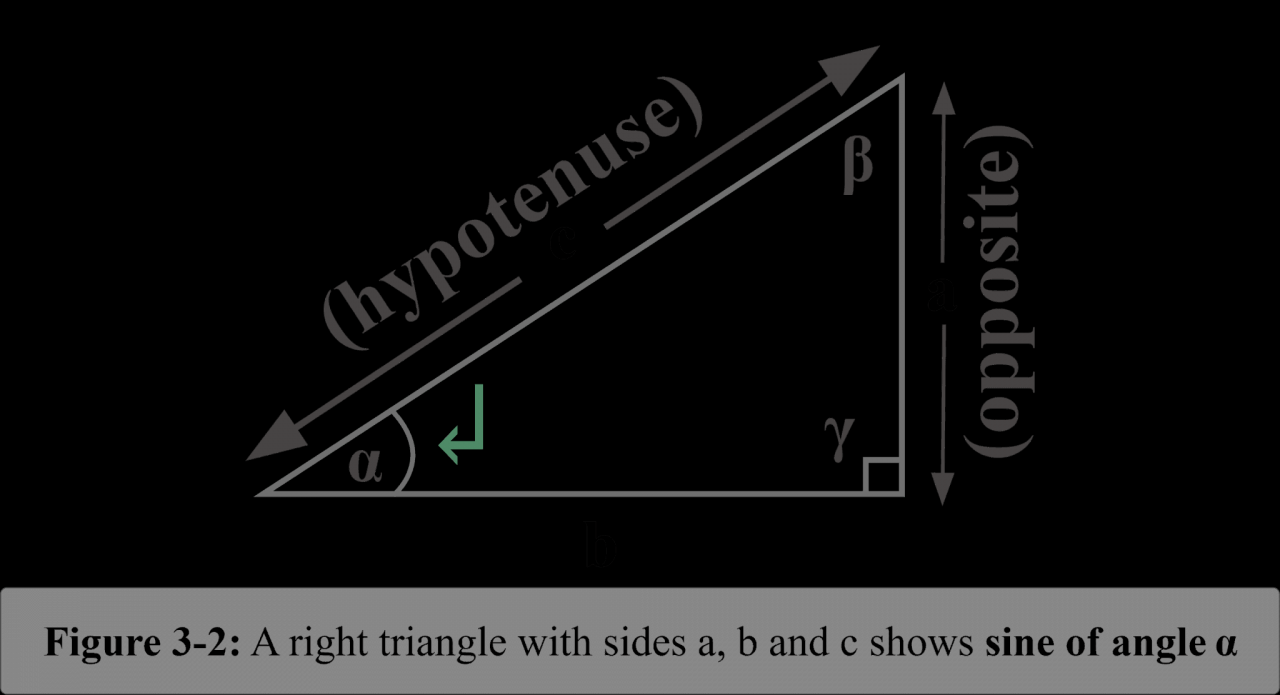
The sine function, denoted as sin(x), is a fundamental trigonometric function that plays a crucial role in various fields. It is defined as the ratio of the length of the opposite side to the length of the hypotenuse in a right triangle with an angle x.

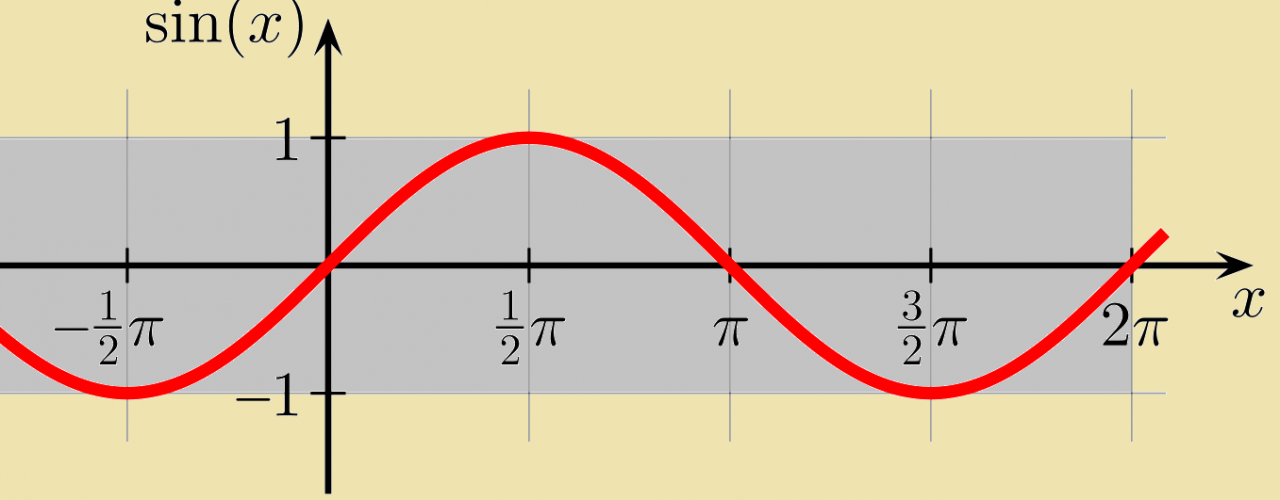
The range of the sine function is [-1, 1], and its period is 2π. This means that the function repeats itself every 2π units.

Examples of Sine Function Graphs

• y = sin(x): A basic sine function graph that oscillates between -1 and 1.
• y = 2sin(x): A sine function graph with a vertical stretch of 2, resulting in a larger amplitude.
• y = sin(2x): A sine function graph with a horizontal compression of 2, resulting in a narrower period.

Sine Function Properties

The sine function possesses several key properties that make it useful in applications:

Periodicity

The sine function is periodic with a period of 2π. This means that sin(x) = sin(x + 2π) for all x.

Symmetry

The sine function is an odd function, meaning that sin(-x) = -sin(x).

Extrema

The sine function has a maximum value of 1 at x = π/2 + 2πn and a minimum value of -1 at x = 3π/2 + 2πn, where n is an integer.

Relationship with Other Trigonometric Functions

The sine function is closely related to other trigonometric functions, such as cosine and tangent:

• cos(x) = sin(π/2 – x)
• tan(x) = sin(x) / cos(x)

Applications of the Sine Function

The sine function has numerous applications in various fields:

Physics

• Modeling simple harmonic motion, such as the oscillation of a pendulum.
• Analyzing sound waves, as the amplitude of a sound wave can be represented by a sine function.

Engineering, Sine definition

• Designing structures that can withstand periodic forces, such as wind or earthquake loads.
• Creating electrical circuits that generate alternating currents, which are essential for power transmission.

Music

• Determining the pitch of musical notes, as the frequency of a note is proportional to the sine function.
• Creating musical instruments, such as string instruments and wind instruments, which produce sounds based on the sine function.

Sine Function in Calculus

The sine function is differentiable and integrable:

Differentiation

The derivative of the sine function is the cosine function: sin'(x) = cos(x).

Integration

The integral of the sine function is the negative cosine function: ∫sin(x) dx = -cos(x) + C, where C is the constant of integration.

Applications in Calculus Problems

• Finding the velocity and acceleration of an object undergoing simple harmonic motion.
• Calculating the area under a sine function curve.
• Solving differential equations involving the sine function.

Inverse Sine Function

The inverse sine function, denoted as sin^-1(x), is the inverse of the sine function. It is defined as the angle whose sine is x.

Properties and Applications

• The range of the inverse sine function is [-π/2, π/2].
• The inverse sine function is used to find the angle of a right triangle given the ratio of the opposite side to the hypotenuse.
• It is also used in navigation, astronomy, and other fields where angle calculations are necessary.

Final Wrap-Up: Sine Definition

In closing, the sine function emerges as a cornerstone of mathematics, indispensable in modeling periodic phenomena, understanding calculus concepts, and unlocking real-world applications. Its versatility and elegance continue to inspire awe and drive scientific advancements.

Query Resolution

What is the mathematical definition of the sine function?

The sine function is defined as the ratio of the length of the opposite side to the length of the hypotenuse in a right triangle.

What is the range and period of the sine function?

The range of the sine function is [-1, 1], and its period is 2π.

What are some real-world applications of the sine function?

The sine function is used in a wide variety of applications, including modeling sound waves, tides, and the motion of objects in periodic motion.